CCSS Objective N.RN.1
Explain how the definition of the meaning of rational exponents follows from extending the properties of integer exponents to those values, allowing for a notation for radicals in terms of rational exponents.
For example, we define 51/3 to be the cube root of 5 because we want (51/3)3 = 5(1/3)3 to hold, so (51/3)3 must equal 5.
Ready
Hints for problems 1 - 9.
If you haven't already done so, create a list of perfect squares (1, 4, 9, 16, 25, …) and perfect cubes (1, 8, 27, 64, …) along the edge of your paper to so that you'll know which factors to try use as much as possible when factoring each radical expression. The terms inside the radical are called the "radicand". Always try to re-express the radicand into factors that fit the square root or the cube root (or the 5th root for problem #7). Then pull that factor outside the radical sign and rewrite it as a smaller term.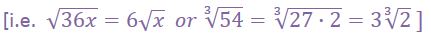 
Set
Hints for problems 10 - 12.
Since these three problems are all designated as arithmetic sequences, then the explicit equation learned earlier in the year should be quite handy.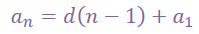 
can be used for each of the three problems because the first term (a1) is given in each problem as well as an nth term in each table. By plugging those known terms into the explicit form of the equation for arithmetic sequences, then you should be able to solve for the common difference. By using the common difference, just keep adding that amount to the previous term in the table. If you're really adventurous, you'll explore other shortcuts for determining the missing values in each table.
Hints for problems 13-15.
Use the same process as explained above, but rely on the explicit form of the geometric equation which is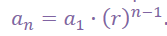 
. Through trial and error if necessary, you should be able to solve for the "base" of r when given the other terms that are all contained in the table. Once you have r, then you can just multiply the previous term by your newly discovered r to build the next term.
Hints for problems 16 - 18.
Try to use only the arrows that indicate the whole number increments first while ignoring the Fc factors. Once you've completed the whole number increments, then go back to fill in the cells aligned with the Fc factors. If the two cells on either side of an empty cell are filled, then utilize the quick method of finding a geometric mean between two numbers by multiplying the two numbers together, then finding the square root of the product. This will likely result in a number that includes a 
sign. Be sure to simplify your answers as far as possible like you did in problems 1 - 9.
Go
Hints for problems 19 - 24.
This section of the assignment is excellent for strengthening your computational skills once you've correctly understood all the function notation being used. Each problem gives you a function (like a road map) along with three parts (a, b, and c) below it that are essentially asking you details about the map. Remember that any number given inside a set of parentheses is the input number, while any number given alongside an equal sign and following an "f(x)=" is the output number. Some of these problems can be referred to as "plug & chug" problems, while others work in the opposite direction - you're given the output value and you have to work backwards to determine what needed to be plugged in to obtain that output. For most of these problems, you'll continue to find patterns that will help you to solve for the unknown.
A video tutorial for all of the parts a and c in these problems.